
Investment for safeguarding the value of money is a crucial and delicate decision. Investors seek to learn every possible way to analyse an investment. Capital budgeting techniques are the most feasible tool for this analysis. They help consider factors such as cash flow, time value of money, inflation rate or cost of capital. However, less people know about it.
Net Present Value (NPV) is the measure to calculate the present value of future cash flow to ascertain the payout of an investment. On the other hand, the internal rate of return is obtained by making NPV zero.
Investors usually get confused when selecting the appropriate method between NPV and IRR. However, one should understand the meaning and application of these techniques to decide between NPV vs IRR.
Check this out! Time value of money: calculation and formula
What is Net Present Value (NPV)?
The time value of money depreciates the value of money over a period. Things that ₹10 can buy in the present may not be possible after some years, and it would need more money. We commonly know this as inflation!
Hence, investors should determine the future value of their investment in the present and plan it accordingly. NPV is helpful for such requirements. It is the difference between the present value of cash flows for the investment and its required initial investment. It indicates the profitable standing of an investment.
Calculation of NPV
- Step 1: Discount the future cash outflows
Formula = Cash outflow / (1+r)^t
Here, ‘r’ is the discount rate. It can be the cost of capital, cost of equity or any other specific rate. ‘t’ is the period (year of outflow).
- Step 2: Aggregate all these discounted cash outflows from the investment.
- Step 3: Subtract the initial investment from this sum.
(Example is explained further in the article)
What is IRR?
NPV and IRR are intertwined in a way. The discount rate at which the difference between the present value of cash outflow and the investment is eliminated is the internal rate of return. At this rate, NPV is zero.
It is used to compare the cost of capital or determine the profit. The rationale is that the rate that my investment is offering should be more than my cost. Thus, it is better when IRR is more than the cost of capital, and such investments may be profitable.
Calculation of IRR
It uses the NPV to calculate the rate at which the difference would be zero. So, the calculation is done by trial and error method. MS Excel and Google spreadsheets have this function to smoothen the calculation process.
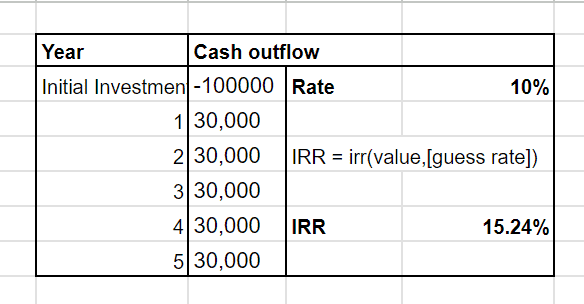
- In Excel or spreadsheet, add your future cash flows for particular years, initial investment (in negative, as cash outflow) and your discount rate.
- Then calculate IRR with its function.
IRR function is : =IRR(values, [guess rate])
Where,
Values are cash flows from investment and initial investment
Guess rate is the discount rate for future values.
So for NPV, we use the cost of capital as a discount rate, and for IRR, we determine such different rates to determine the IRR.
Investors must read this: What does XIRR mean in stock investing?
NPV vs IRR difference
- Meaning
NPV is the difference between the present value of outflows from investment and the initial investment needed.
IRR is the discount rate, where the present cash flow value is equal to the investment and NPV is zero.
- Rate of return
The discount rate, for calculation of the present value from the given future outflow of the investments, will be used. It can be the cost of capital.
Among all the discount rates used to calculate the NPV, the rate at which its difference is zero is the internal rate of return.
- Representation
NPV is the absolute difference, while the IRR is the % form of this difference.
- Formulas
NPV formula = [Cash outflows/(1+r)^t] – Initial investment
There is no set formula for IRR. It is calculated by the trial and error method with different discount rates.
- Interpretation
When NPV is positive, the investment would provide a surplus and vice versa.
When IRR is more than the cost of capital (the discount rate used), it is favourable as the investment return would beat the capital cost.
- Impact
When there is any change in the cash outflows, there is no considerable difference as it would be discounted by the cost of capital. However, in IRR, the perfect rate at which the difference becomes zero may change.
Let’s understand with an example.
An investment has an estimated cash outflow of ₹30,000, for each of the next five years. The investment for this is ₹1 lakhs. The cost of capital for this return is 10%.
Discounting factor = 1/(1+10%)^year
Present value of cash outflow = cash outflow*discounting factor
| Year | Cash outflow | Discounting factor | Present value of cash outflow |
| 1 | ₹30,000 | 0.909 | ₹27,270 |
| 2 | ₹30,000 | 0.826 | ₹24,780 |
| 3 | ₹30,000 | 0.751 | ₹22,530 |
| 4 | ₹30,000 | 0.683 | ₹20,490 |
| 5 | ₹30,000 | 0.621 | ₹18,630 |
| TOTAL | = ₹1,13,700 | ||
| Net Present Value | = ₹1,13,700 – ₹1,00,000= ₹13,700 | ||
(discounting factor approximated till three digits after decimal)
Here, the NPV is positive, and the value of cash outflow is more than the initial investment. So, the project is profitable.
Similarly, we need to determine the rate at which this difference is zero. Through trial and error methods, the IRR is calculated. For the above example, the IRR is 15.24%.
Bottomline
Capital budgeting techniques help evaluate and compare different investments (projects) by their crucial financial metric like cash flow. You can also read about advanced budgeting techniques to improve your personal finance. The NPV helps determine the absolute profitable difference between the present value of expected cash outflow and initial investment. While IRR is the rate obtained by trial and error, the discount rate at which the NPV value or the difference is zero.
To determine the better options between NPV vs IRR, the investors should try evaluating both to obtain the suitable absolute value and the suitable discount rate.
You can also read about: Use these advanced budgeting techniques to save money
FAQs
Q1. Why does IRR set NPV for zero?
The difference between the present value of expected cash flow from the investment and its initial investment is the NPV. So, when they are equal, it indicates the return would be equal to the discounting rate of the money. Thus, IRR is the rate which keeps NPV at zero.
Q2. What happens to NPV when IRR is increased?
IRR is the discount rate, which makes the NPV zero. So, if IRR is more than the cost of capital, the investment is considered attractive. When the IRR increases, the NPV will reduce. IRR is a discount rate. So, when this discount rate increases, future value will be discounted more and such aggregate discounted present value will result in a decrease in NPV.
Q3. Why do firms prefer NPV over IRR?
NPV is the absolute representation of the profitability of an investment. IRR is the ideal rate for an investment to reach a breakout point. Some investors prefer NPV as it can indicate an approx profitable amount, and to evaluate by IRR, there is a need for cost of capital. However, if the capital cost is available, investors can evaluate the profitability of a project by IRR.
Q4. What does IRR tell you?
The discount rate, which eliminates the difference between the present value of future cash flows and the initial investment is the internal rate of return. Thus, it would be when NPV is at zero. IRR greater than the cost of capital is favourable and indicates the profitable nature of investment according to its cash flow.
Q5. What is the rule of thumb for IRR?
There is no set rule of thumb for an ideal IRR. Considering only IRR may not be a clear indication of profitability. However, when the IRR (discount rate) is more than the cost of capital, it indicates that the venture (investment) may be profitable. Similarly, when IRR is less than the cost of capital, in the long run (period of cash flow), the provided discount rate may not be favourable.

