
The Black-Scholes model has the reputation for being a guiding star in the derivatives trading market. Formulated by Fischer Black, Myron Scholes, and Robert Merton back in the early ’70s, the model can look like it came right out of a spellbook, but it’s been a game changer in how investors navigate financial markets.
In this article, we’re going to find out what it is, how it helps traders, and whether it has any limitations. Let’s go!
Understanding the Black-Scholes model
The Black Scholes model is usually used to get a theoretical worth estimate of European-style options. The formula is used to show if an option has a unique price given the risk associated with the underlying security and its expected normal return.
The model is widely used in derivatives trading, especially with options. Since the assumptions in the model are wide and generalised, they have been tweaked over time and have a plethora of niche applications. They are used in derivative pricing and risk management too.
You may also like: The significance of Porter’s five forces model
History
The Black-Scholes model is the first widely used mathematical method to calculate the theoretical value of an options contract. This was initially done using current stock prices, expected dividends, the option’s strike price, expected interest rates, time to expiration, and the level of volatility expected in the stock.
The model received worldwide recognition and praise. Scholes and Merton were awarded the Nobel Memorial Prize in Economic Sciences for their work on the formula in 1997.
The ingredients
The model requires five variables. These inputs are:
- Stock Price (S): Cost per share.
- Strike Price (K): This is the price you have the option to sell or buy the stock until the expiration date.
- Time to Expiration (T): This is how much you still have before your option expires.
- Interest Rate (r): The money you could make if you invested your cash somewhere else instead of buying this option.
- Volatility (σ): How much the prices of the thing you’re trading jump around.
There are also some assumptions that the model makes:
- No dividends are paid out to the holder during the lifetime of the option.
- The risk-free rate and volatility of the stock in the formula are known, accurate, and constant. (This is also a limitation, explained later)
- The returns of the underlying stock are normally distributed.
- Markets are random and price movements can’t be accurately and reasonably predicted.
- There are no transaction costs involved while buying this option from the buy side.
Also Read: Interest rate risk – Meaning and risk management strategies.
The formula
The math used in the Black-Scholes formula can, to the layman, seem complicated and overwhelming. Fortunately, most people don’t need to understand the context and work behind the formula to use it well.
Today, most online calculators and spreadsheets have made using the formula much easier; in fact, most people who use this formula regularly to create analyses don’t ever see it in its true form.
However, for the sake of covering all bases, we’re going to take a brief look at the formula and identify the key variables:
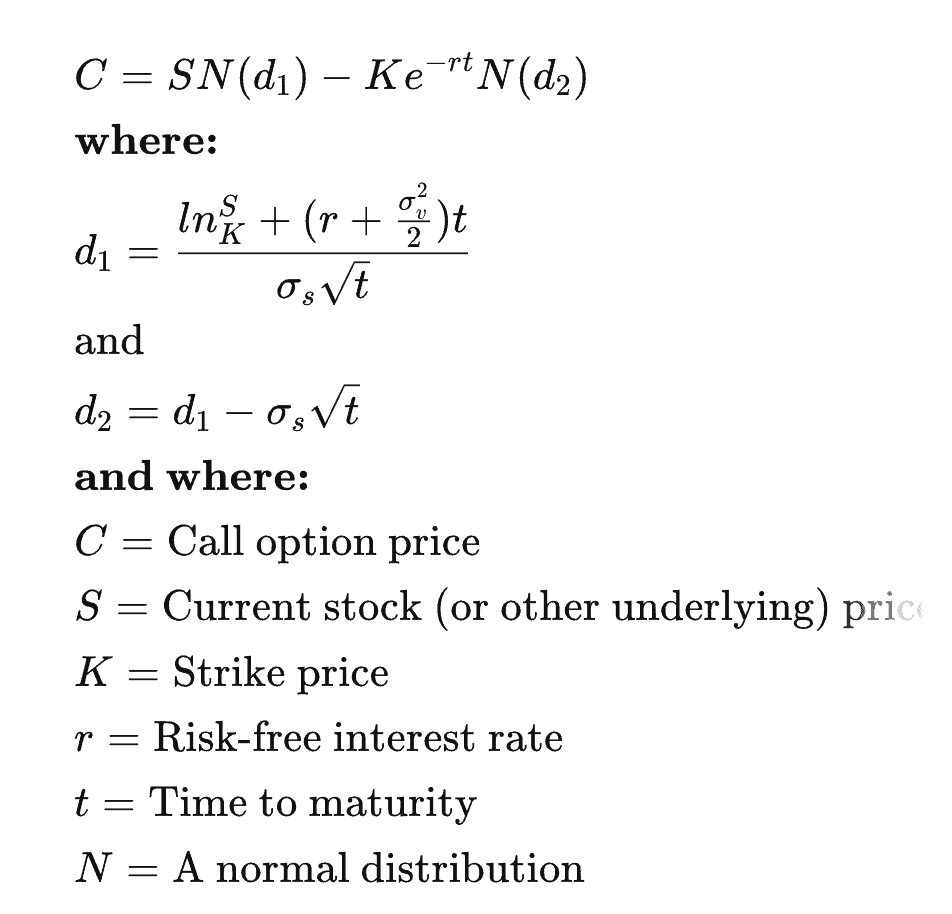
Using the Black-Scholes model
- Calculating option prices – You can use the Black-Scholes model to calculate how much a call option should cost to you based on the variables used in the formula. It takes into account the time value of the option, the strike price, and the price you’re paying.
- Risk management – The model can also be used to understand the risks associated with a particular options trade and make more informed decisions.
- Financial innovation by influencing market products – By being used in various applications in the finance sector, this model has also, in a way, helped in the development and innovation of novel financial products and strategies that would otherwise have never been formulated.
Also Read: Covered calls: The silent strategy fueling top portfolios
Limitations of the Black-Scholes model
Like with any other trading financial framework, the Black-Scholes model also has its limitations:
- Assumes constant volatility – The model assumes that the volatility of an underlying stock remains constant over a certain amount of time. While that might sometimes be the case, volatility can be unpredictable too.
Factors like news, special events, or market sentiment significantly affect volatility. This limitation implies that the model might not accurately predict option prices when volatility rates are unstable. - Assumes high liquidity – The model also assumes that you can always buy or sell the underlying asset at any quantity without affecting the market price, and that couldn’t be farther from the truth in illiquid markets where executing trades can be challenging.
- Limited mostly to European-style options – The Black-Scholes model was developed primarily for European-style options, which can only be exercised at expiry. The framework is less effective for American-style options which can be exercised anytime before expiry.
Conclusion
In conclusion, the Black-Scholes model is a valuable tool for option pricing, but it has several limitations that could impact its accuracy in several real-world applications.
While the model is one that’s been repeatedly tested over time, investors must stay wary of its limitations and exercise its results with caution.

